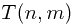You can add multiple items of the same type to the knapsack.
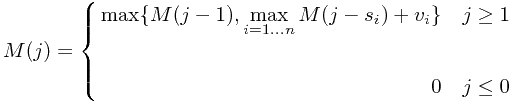
Computing each 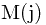 value will require
value will require 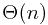 time, and we need to sequentially compute
time, and we need to sequentially compute 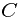 such values.
such values.
Therefore, total running time is 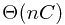 . Total space is
. Total space is 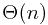 .
.
The value of 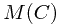 will contain the value of the optimal knapsack packing.
will contain the value of the optimal knapsack packing.
We can reconstruct the list of items in the optimal solution by maintaining and following “backpointers”
2. Maximum Value Contiguous Subsequence.
Given a sequence of  real numbers
real numbers 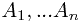 ,
,
determine a contiguous subsequence 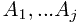 for which the sum of elements in the subsequence is maximized.
for which the sum of elements in the subsequence is maximized.
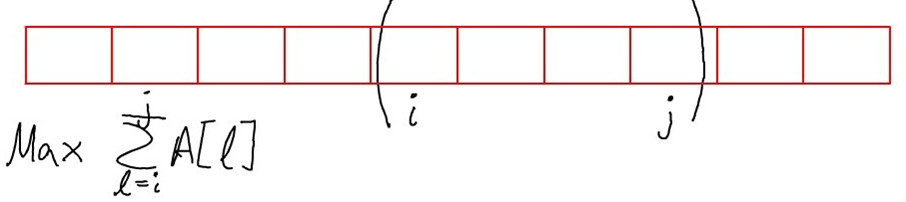
Solution: Let 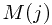 denote the max sum over all windows ending at
denote the max sum over all windows ending at 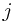
![$M(j) = max\{ M(j-1)+A[j], A[j]\}$ $M(j) = max\{
M(j-1)+A[j], A[j]\}$](/user_files/guitarpenguin/epics/75df234a406bdd23652cee38ca1d10473cf0307d.png)
It only takes linear time 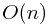 to run the program since it only need to solve
to run the program since it only need to solve  sub-problems and each takes constnt time.
sub-problems and each takes constnt time.
3. Making Change: You are given  types of coin denominations of values
types of coin denominations of values 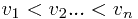 (all integers).
(all integers).
Assume  , so you can always make change for any amount of money C.
, so you can always make change for any amount of money C.
Give an algorithm which makes change for an amount of money C with as few coins as possible.
Solution: Let 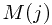 denote the min number of coins required to make changes for amount of money
denote the min number of coins required to make changes for amount of money 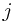
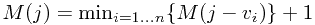
It takes 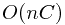 time because we are solving
time because we are solving 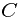 subproblems,
subproblems,
each of which requires minimization 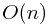 different terms. (Similar to integer knapsack problem)
different terms. (Similar to integer knapsack problem)
4. Longest Increasing Subsequence. Given a sequence of n real numbers 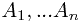 ,
,
determine a subsequence (not necessarily contiguous) of maximum length in which the values in the subsequence form a strictly increasing sequence.

Solution: Let 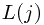 denote the longest strictly increasing subsequence ending at position
denote the longest strictly increasing subsequence ending at position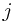 , therefore,
, therefore,
![$L(j) = \max\limits_{i<j}\limits_{A[i]<A[j]}\{ L(i)\}+1
$ $L(j) =
\max\limits_{i<j}\limits_{A[i]<A[j]}\{ L(i)\}+1 $](/user_files/guitarpenguin/epics/94b81961bce2dcc29340c502e9f246b6461be9cd.png)
to find the solution overall, it has to find the maximum over all potential ending points 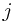 of
of 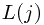 :
:
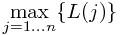
since the longest increasing subsequence could end anywhere.
The algorithm takes 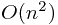 time to run because I have to sort
time to run because I have to sort  subproblems and each of them takes
subproblems and each of them takes 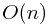 time.
time.
5.Box Stacking:
You are given a set of  types of rectangular 3-D boxes, where the
types of rectangular 3-D boxes, where the 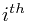 box has height
box has height 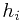 , width
, width 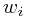 and depth
and depth  (all real numbers).
(all real numbers).
You want to create a stack of boxes which is as tall as possible,
but you can only stack a box on top of another box if the dimensions of the 2-D base of the lower box are each strictly larger than those of the 2-D base of the higher box.
Of course, you can rotate a box so that any side functions as its base.
It is also allowable to use multiple instances of the same type of box.
Solution: constraint : can only stack box 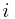 on box
on box 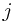 if
if 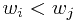 and
and 
(without loss of generality, assume  ).
).
First sort the base area by decreasing order:

then let 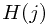 denote the tallest box stack I could form with box
denote the tallest box stack I could form with box 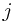 on top, so
on top, so
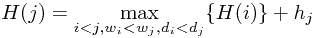
The algorithm takes 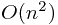 time to run because I have to sort
time to run because I have to sort  subproblems and each of them takes
subproblems and each of them takes 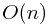 time.
time.
At the end, the solution is found by taking the max of all potential top boxes 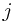 of
of 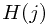 .
.
(Since we are not sure in the optimal solution, which box is on top)
6. Building Bridges.
Consider a 2-D map with a horizontal river passing through its center.
There are  cities on the southern bank with x-coordinates
cities on the southern bank with x-coordinates  and
and  cities on the northern bank with x-coordinates
cities on the northern bank with x-coordinates 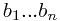 .
.
You want to connect as many north-south pairs of cities as possible with bridges such that no two bridges cross.
When connecting cities, you are only allowed to connect the the ith city on the northern ban to the ith city on the southern bank.
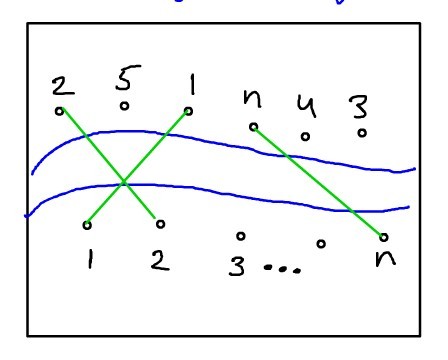
Solution: consider the south bank city (below the river) 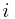 ,
,
let 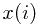 denote the index of corresponding city on the north bank (
denote the index of corresponding city on the north bank (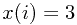 in the figure).
in the figure).
So we could compute the 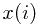 by sorting in
by sorting in  time.
time.
Now we want to find the longest increasing subsequence through 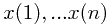 , so it is identical to problem 4.
, so it is identical to problem 4.
7. Balanced Partition:You have a set of n integers each in the range 0 . . .K.
Partition these integers into two subsets such that you minimize  ,
,
where 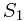 and
and 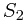 denote the sums of the elements in each of the two subsets.
denote the sums of the elements in each of the two subsets.
Solution: Use 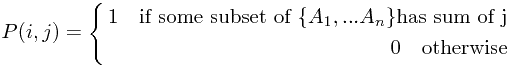 where
where ![$i \in [0,n]$ $i \in [0,n]$](/user_files/guitarpenguin/epics/ae942c2c789f8c49c896fa7c19724c64c85b71b5.png) and
and ![$j \in [0,nK]$ $j \in
[0,nK]$](/user_files/guitarpenguin/epics/8158ca2fb382567f6418f95fbdfe2e245042f17e.png)
therefore, 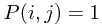 if
if 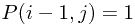 or
or 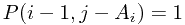
dynamic programming formula is:

this procedure takes 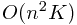 time to compute.
time to compute.
To solve the original problem, let 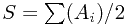 , and the purpose is to make
, and the purpose is to make  close to 0 as possible.
close to 0 as possible.
what we want to find is:
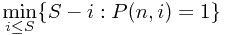
8. Edit Distance.
Given two text strings A of length n and B of length m,
you want to transform A into B with a minimum number of operations of the following types:
delete a character from A, insert a character into A,
or change some character in A into a new character.
The minimal number of such operations required to transform A into B is called the edit distance between A and B.
Solution: Use  to denote the cost for inserting, deleting or replacing a letter.
to denote the cost for inserting, deleting or replacing a letter.
The goal is to compute the minimum cost of translating A to B.
Let 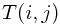 denote the minimum cost of translating
denote the minimum cost of translating ![$A[1...i]$ $A[1...i]$](/user_files/guitarpenguin/epics/bec246f17119e8bdcb5bbfbaec3019b85b30ba74.png) into
into ![$B[1...j]$ $B[1...j]$](/user_files/guitarpenguin/epics/820b6767f72026f28422f5e27e3c0fb0fe832c62.png) , then
, then
![$$T(i,j)= \left\{\begin{aligned}\overset{}C_d + T(i-1, j) \\
C_i+T(i, j-1) \\ \overset{} T(i-1, j-1) \quad if \quad A[i]=B[j] \\
C_d+T(i-1,j-1) \quad if \quad A[i] \neq B[j] \end{aligned}\right.$$ $$T(i,j)= \left\{\begin{aligned}\overset{}C_d + T(i-1, j) \\
C_i+T(i, j-1) \\ \overset{} T(i-1, j-1) \quad if \quad A[i]=B[j] \\
C_d+T(i-1,j-1) \quad if \quad A[i] \neq B[j] \end{aligned}\right.$$](/user_files/guitarpenguin/epics/86361303bd84efa6c5640a655cbbace1642d4ca0.png)
It takes 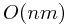 time to compute and final solution is stored in
time to compute and final solution is stored in 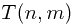
 types of items, where the
types of items, where the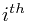 item type has an integer size
item type has an integer size  and a real value.
and a real value. 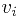
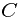 with a selection of items of maximum value.
with a selection of items of maximum value.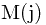 denote the maximum value you can pack into a size
denote the maximum value you can pack into a size 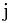 knapsack.
knapsack.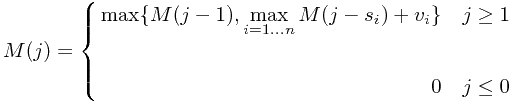
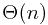 time, and we need to sequentially compute
time, and we need to sequentially compute 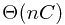 . Total space is
. Total space is 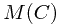 will contain the value of the optimal knapsack packing.
will contain the value of the optimal knapsack packing.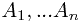 ,
,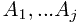 for which the sum of elements in the subsequence is maximized.
for which the sum of elements in the subsequence is maximized.
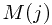 denote the max sum over all windows ending at
denote the max sum over all windows ending at 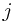
![$M(j) = max\{ M(j-1)+A[j], A[j]\}$ $M(j) = max\{
M(j-1)+A[j], A[j]\}$](/user_files/guitarpenguin/epics/75df234a406bdd23652cee38ca1d10473cf0307d.png)
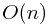 to run the program since it only need to solve
to run the program since it only need to solve 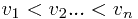 (all integers).
(all integers). , so you can always make change for any amount of money C.
, so you can always make change for any amount of money C.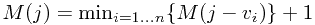
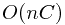 time because we are solving
time because we are solving 
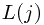 denote the longest strictly increasing subsequence ending at position
denote the longest strictly increasing subsequence ending at position![$L(j) = \max\limits_{i<j}\limits_{A[i]<A[j]}\{ L(i)\}+1
$ $L(j) =
\max\limits_{i<j}\limits_{A[i]<A[j]}\{ L(i)\}+1 $](/user_files/guitarpenguin/epics/94b81961bce2dcc29340c502e9f246b6461be9cd.png)
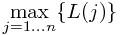
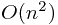 time to run because I have to sort
time to run because I have to sort 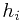 , width
, width 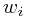 and depth
and depth  (all real numbers).
(all real numbers).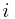 on box
on box 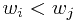 and
and 
 ).
).
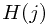 denote the tallest box stack I could form with box
denote the tallest box stack I could form with box 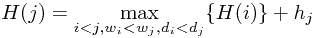
 and
and 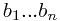 .
.
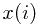 denote the index of corresponding city on the north bank (
denote the index of corresponding city on the north bank (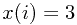 in the figure).
in the figure). time.
time.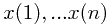 , so it is identical to problem 4.
, so it is identical to problem 4. ,
,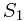 and
and 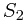 denote the sums of the elements in each of the two subsets.
denote the sums of the elements in each of the two subsets.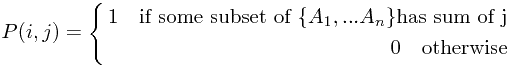 where
where ![$i \in [0,n]$ $i \in [0,n]$](/user_files/guitarpenguin/epics/ae942c2c789f8c49c896fa7c19724c64c85b71b5.png) and
and ![$j \in [0,nK]$ $j \in
[0,nK]$](/user_files/guitarpenguin/epics/8158ca2fb382567f6418f95fbdfe2e245042f17e.png)
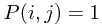 if
if 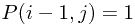 or
or 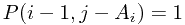

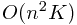 time to compute.
time to compute.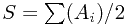 , and the purpose is to make
, and the purpose is to make 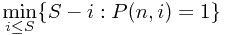
 to denote the cost for inserting, deleting or replacing a letter.
to denote the cost for inserting, deleting or replacing a letter.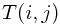 denote the minimum cost of translating
denote the minimum cost of translating ![$A[1...i]$ $A[1...i]$](/user_files/guitarpenguin/epics/bec246f17119e8bdcb5bbfbaec3019b85b30ba74.png) into
into ![$B[1...j]$ $B[1...j]$](/user_files/guitarpenguin/epics/820b6767f72026f28422f5e27e3c0fb0fe832c62.png) , then
, then![$$T(i,j)= \left\{\begin{aligned}\overset{}C_d + T(i-1, j) \\
C_i+T(i, j-1) \\ \overset{} T(i-1, j-1) \quad if \quad A[i]=B[j] \\
C_d+T(i-1,j-1) \quad if \quad A[i] \neq B[j] \end{aligned}\right.$$ $$T(i,j)= \left\{\begin{aligned}\overset{}C_d + T(i-1, j) \\
C_i+T(i, j-1) \\ \overset{} T(i-1, j-1) \quad if \quad A[i]=B[j] \\
C_d+T(i-1,j-1) \quad if \quad A[i] \neq B[j] \end{aligned}\right.$$](/user_files/guitarpenguin/epics/86361303bd84efa6c5640a655cbbace1642d4ca0.png)
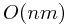 time to compute and final solution is stored in
time to compute and final solution is stored in